Uji heteroskedastisitas digunakan untuk mengetahui ada atau tidaknya penyimpangan asumsi klasik heteroskedastisitas yaitu adanya ketidaksamaan varian dari residual untuk semua pengamatan pada model regresi. Prasyarat yang harus terpenuhi dalam model regresi adalah tidak adanya gejala heteroskedastisitas. Ada beberapa metode pengujian yang bisa digunakan diantaranya yaitu Uji Park, Uji Glesjer, Melihat pola grafik regresi, dan uji koefisien korelasi Spearman.
a) Uji Park
Metode uji Park yaitu dengan meregresikan nilai logaritma natural dari residual kuadrat (Lne2) dengan variabel independen (X1 dan X2).
a) Uji Park
Metode uji Park yaitu dengan meregresikan nilai logaritma natural dari residual kuadrat (Lne2) dengan variabel independen (X1 dan X2).
Kriteria pengujian adalah sebagai berikut:
1. Ho : tidak ada gejala heteroskedastisitas
2. Ha : ada gejala heteroskedastisitas
3. Ho diterima bila Signifikansi > 0,05 berarti tidak terdapat heteroskedastisitas dan Ho ditolak bila Signifikansi < 0,05 yang berarti terdapat heteroskedastisitas.
b) Uji Glejser
Uji Glejser dilakukan dengan cara meregresikan antara variabel independen dengan nilai absolut residualnya (ABS_RES). Jika nilai signifikansi antara variabel independen dengan absolut residual lebih dari 0,05 maka tidak terjadi masalah heteroskedastisitas.
Uji Glejser dilakukan dengan cara meregresikan antara variabel independen dengan nilai absolut residualnya (ABS_RES). Jika nilai signifikansi antara variabel independen dengan absolut residual lebih dari 0,05 maka tidak terjadi masalah heteroskedastisitas.
Contoh kasus:
Akan dilakukan analisis regresi linier berganda untuk mengetahui pengaruh biaya produksi, distribusi, dan promosi terhadap tingkat penjualan. Dengan ini sebelumnya akan dilakukan uji asumsi klasik heteroskedastisitas dengan metode uji Glejser. Data sebagai berikut:
Tahun
|
Tingkat penjualan
|
Biaya produksi
|
Biaya distribusi
|
Biaya promosi
|
1996
|
127300000
|
37800000
|
11700000
|
8700000
|
1997
|
122500000
|
38100000
|
10900000
|
8300000
|
1998
|
146800000
|
42900000
|
11200000
|
9000000
|
1999
|
159200000
|
45200000
|
14800000
|
9600000
|
2000
|
171800000
|
48400000
|
12300000
|
9800000
|
2001
|
176600000
|
49200000
|
16800000
|
9200000
|
2002
|
193500000
|
48700000
|
19400000
|
12000000
|
2003
|
189300000
|
48300000
|
20500000
|
12700000
|
2004
|
224500000
|
50300000
|
19400000
|
14000000
|
2005
|
239100000
|
55800000
|
20200000
|
17300000
|
2006
|
257300000
|
56800000
|
18600000
|
18800000
|
2007
|
269200000
|
55900000
|
21800000
|
21500000
|
2008
|
308200000
|
59300000
|
24900000
|
21700000
|
2009
|
358800000
|
62900000
|
24300000
|
25900000
|
2010
|
362500000
|
60500000
|
22600000
|
27400000
|
Langkah-langkah analisis pada SPSS sebagai berikut:
- Inputkan data di SPSS
- Langkah pertama yaitu mencari nilai unstandardized residual, caranya klik Analyze >> Regression >> Linear
- Pada kotak dialog Linear Regression, masukkan variabel Tingkat penjualan ke kotak Dependent, kemudian masukkan variabel Biaya produksi, Biaya distribusi, dan Biaya promosi ke kotak Independent(s).
- Klik tombol Save, selanjutnya akan terbuka kotak dialog ‘Linear Regression: Save’
- Pada Residuals, beri tanda centang pada ‘Unstandardized’. Kemudian klik tombol Continue. Akan kembali ke kotak dialog sebelumnya, klik tombol OK. Hiraukan hasil output SPSS, Anda buka input data, disini akan bertambah satu variabel yaitu residual (RES_1).
- Langkah selanjutnya mencari nilai absolute residual dari nilai residual di atas, caranya klik menu Transform >> Compute Variable.
- Pada kotak Target Variable, merupakan nama variabel baru yang akan tercipta. Ketikkan ABS_RES (absolute residual). Kemudian klik pada kotak Numeric Expression, lalu ketikkan ABS( lalu masukkan variabel Unstandardized Residual (RES_1) ke kotak Numeric Expression dengan klik tanda penunjuk, kemudian ketik tanda tutup kurung. Maka lengkapnya akan tertulis ABS(RES_1), perintah ini untuk menghitung nilai absolute dari residual. Jika sudah klik tombol OK.
- Langkah selanjutnya meregresikan nilai variabel independen dengan absolute residual. Caranya klik Analyze >> Regression >> Linear.
- Masukkan variabel ABS_RES ke kotak Dependent, kemudian masukkan varibel Biaya produksi, Biaya distribusi, dan Biaya promosi ke kotak Independent(s). Selanjutnya klik tombol OK. Maka hasil pada output Coefficient seperti berikut:
Dari output di atas dapat diketahui bahwa nilai signifikansi ketiga variabel independen lebih dari 0,05. Dengan demikian dapat disimpulkan bahwa tidak terjadi masalah heteroskedastisitas pada model regresi.
c) Melihat pola titik-titik pada scatterplots regresi
Metode ini yaitu dengan cara melihat grafik scatterplot antara standardized predicted value (ZPRED) dengan studentized residual (SRESID). Ada tidaknya pola tertentu pada grafik scatterplot antara SRESID dan ZPRED dimana sumbu Y adalah Y yang telah diprediksi dan sumbu X adalah residual (Y prediksi - Y sesungguhnya).
Dasar pengambilan keputusan yaitu:
- Jika ada pola tertentu, seperti titik-titik yang ada membentuk suatu pola tertentu yang teratur (bergelombang, melebar kemudian menyempit), maka terjadi heteroskedastisitas.
- Jika tidak ada pola yang jelas, seperti titik-titik menyebar di atas dan di bawah angka 0 pada sumbu Y, maka tidak terjadi heteroskedastisitas.
Langkah-langkah analisis pada SPSS sebagai berikut:
- Inputkan data di SPSS
- Untuk analisis data, klik menu Analyze >> Regression >> Linear
- Pada kotak dialog Linear Regression, masukkan variabel Tingkat penjualan ke kotak Dependent, kemudian masukkan variabel Biaya produksi, Biaya distribusi, dan Biaya promosi ke kotak Independent(s).
- Klik tombol Plots, maka akan terbuka kotak dialog ‘Linear Regression: Plots’.
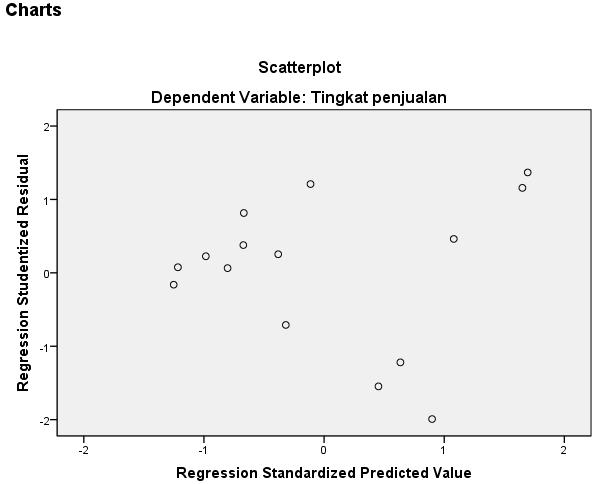
- Klik *SRESID (Studentized Residual) lalu masukkan ke kotak Y dengan klik tanda penunjuk. Kemudian klik *ZPRED (Standardized Predicted Value) lalu masukkan ke kotak X. Jika sudah klik tombol Continue. Akan terbuka kotak dialog sebelumnya, klik tombol OK, maka hasil output pada grafik Scatterplot sebagai berikut:
Dari output di atas dapat diketahui bahwa titik-titik tidak membentuk pola yang jelas, dan titik-titik menyebar di atas dan di bawah angka 0 pada sumbu Y. Jadi dapat disimpulkan bahwa tidak terjadi masalah heteroskedastisitas dalam model regresi.
d) Uji koefisien korelasi Spearman’s rho
Metode uji heteroskedastisitas dengan korelasi Spearman’s rho yaitu mengkorelasikan variabel independen dengan nilai unstandardized residual. Pengujian menggunakan tingkat signifikansi 0,05 dengan uji 2 sisi. Jika korelasi antara variabel independen dengan residual di dapat signifikansi lebih dari 0,05 maka dapat dikatakan bahwa tidak terjadi masalah heteroskedastisitas pada model regresi.
Langkah-langkah analisis pada SPSS sebagai berikut:
- Inputkan data di SPSS
- Langkah pertama yaitu mencari nilai unstandardized residual, caranya klik Analyze >> Regression >> Linear
- Pada kotak dialog Linear Regression, masukkan variabel Tingkat penjualan ke kotak Dependent, kemudian masukkan variabel Biaya produksi, Biaya distribusi, dan Biaya promosi ke kotak Independent(s).
- Klik tombol Save, selanjutnya akan terbuka kotak dialog ‘Linear Regression: Save’
- Pada Residuals, beri tanda centang pada ‘Unstandardized’. Kemudian klik tombol Continue. Akan kembali ke kotak dialog sebelumnya, klik tombol OK. Hiraukan hasil output SPSS, Anda buka input data, disini akan bertambah satu variabel yaitu residual (RES_1).
- Langkah selanjutnya melakukan analisis Spearman’s rho dengan cara klik Analyze >> Correlate >> Bivariate, selanjutnya akan terbuka kotak dialog Bivariate Correlations.
- Masukkan variabel Biaya produksi, Biaya distribusi, Biaya promosi dan Unstandardized Residual ke kotak Variables. Kemudian hilangkan tanda centang pada Pearson dan beri tanda centang pada Spearman. Gambar seperti di atas. Jika sudah klik tombol OK, maka hasil output seperti berikut:
Dari output di atas dapat diketahui bahwa nilai korelasi ketiga variabel independen dengan Unstandardized Residual memiliki nilai signifikansi lebih dari 0,05. Karena signifikansi lebih dari 0,05 maka dapat disimpulkan bahwa tidak terjadi masalah heteroskedastisitas pada model regresi.